Algoritmos Genéticos – Ejemplo
Para descargar el programa con el algoritmo genético que se muestra en esta entrada, lo podeis descargar pinchando AQUI.
Como ya se vio en el post "¿Que es la Computación Evolutiva?", los algoritmos genéticos son un tipo de algoritmos evolutivos que sirven para resolver problemas de optimización y que se diferencia principalmente de los demás tipos de algoritmos evolutivos por la forma de representar a los individuos, que lo hace por medio de cadenas binarias (Arrays binarios).
En esta entrada vamos a poner un ejemplo de como obtener el máximo de la función que se muestra a continuación en el rango de [0-15] utilizando un algoritmo genético (el argumento del seno de la función se da en radianes). En este ejemplo que ponemos, esta función sera la "Función de Fitness" o función de calidad que utilizaremos en este problema, ya que la 'x' que maximize esta función, sera la mejor solución al problema.
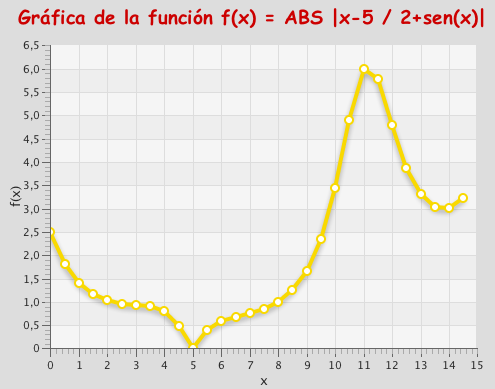
Antes de ver como solucionar el problema, vamos a mostrar en la siguiente imagen la gráfica de esta función para comprobar que el máximo de esta función para el intervalo [0-15] es "x=11" y de esta forma podremos ver lo "bueno o malo" que son los algoritmos genéticos:
El primer "problema" que se nos plantea es "como representar a los individuos" que tendremos en este algoritmo genético. Pues en este caso es muy sencillo y el problema esta planteado adrede para ello. Como en los algoritmos genéticos los individuos se representan con cadenas binarias es muy intuitivo que si queremos encontrar el máximo entre el intervalo [0-15] representemos a los individuos como "números binarios" en este caso como números binarios de longitud 4. Con un numero binario de 4 bits podremos representar 16 números (2^4=16) con lo cual decimos que "los individuos van a estar representados por un cromosoma de longitud 4". Ejemplo:
Una vez llegado a este punto en el que tenemos definida la función de fitness y como representar a los individuos, tenemos que ver: como generamos la primera generación de individuos, como los emparejamos y como mutan. Para realizar todas estas cosas se generará un conjunto de números aleatorios con los que trabajaremos y que veremos su significado a continuación. Para ello y antes de nada deberemos definir con que numero de individuos queremos trabajar, la probabilidad de generación del cromosoma, la probabilidad de emparejamiento y la probabilidad de mutación. Para ver de forma detallada todo este proceso y siguiendo el pseudocódigo mostrado en la entrada de "¿Que es la Computación Evolutiva?" vamos a definir todas estas cosas y ver de forma detallada el transcurso del algoritmo:
- Longitud del cromosoma: 4
- Conjunto de elementos del cromosoma: {0,1}
- Número de individuos de la población: 2
- Para la creación de la primera generación:
3.1.- Probabilidad del elemento '0': num aleatorio < 0.5
3.2.- Probabilidad del elemento '1': num aleatorio >0.5 - Probabilidad de emparejamiento: 0.7
- Probabilidad de mutación: 0.3
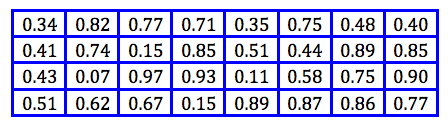
El conjunto de números aleatorios con los que vamos a trabajar va a ser el siguiente:
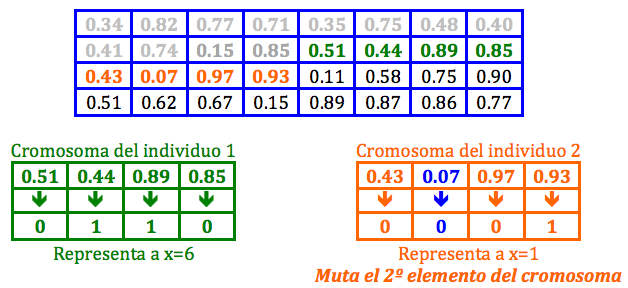
En primer lugar vamos a obtener los dos primeros individuos que van a formar la generación inicial. Para obtener los cromosomas de los dos individuos vamos a utilizar los 8 primeros números aleatorios (4 por individuo). Si el numero aleatorio es menor que 0.5 pondremos el elemento '0' al cromosoma y si es mayor que 0.5 le daremos valor '1'. A continuación mostramos como generamos los individuos:
Una vez que conocemos los individuos, aplicamos la función de fitness para que nos diga que individuo es el mejor de los dos y cuanto mejor es uno que otro para ver posteriormente que probabilidad de emparejamiento tiene cada uno:
Como vemos ambos individuos son muy parecidos porque tienen una calidad similar aunque el individuo 2 es un poco mejor que el individuo 1 ya que lo que pretendemos es encontrar el máximo de la función. Ahora pasamos a calcular las probabilidades de cada individuo para el emparejamiento y esto lo hacemos con una regla de tres simple:
Lo que pretendemos con esto es ver que individuos seleccionamos para emparejarse. Para ello cogeremos los dos siguientes números aleatorios y si están dentro de los rangos de selección, ese individuo sera apto para el emparejamiento (en el caso de que haya emparejamiento es esa generación). Esto quiere decir que si sacamos un número aleatorio dentro del intervalo [0-0.48) el individuo 1 se emparejará y si otro numero aleatorio esta en el intervalo [0.48-1] tambien sera apto el individuo 2 para emparejarse. A continuación vemos si son aptos para emparejarse o no:
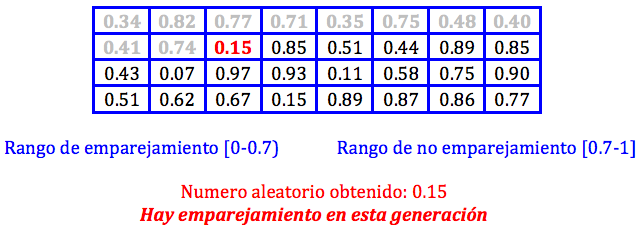
Con esto vemos que los dos individuos son aptos para el emparejamiento, pero ¿habrá emparejamiento en esta generación?. Para ver si en esta generación hay emparejamiento hay que ver si el siguiente numero aleatorio esta dentro de la probabilidad de emparejamiento que la definimos como 0.7, lo que quiere decir que si el número aleatorio esta en el rango [0-0.7) habrá emparejamiento y si esta entre [0.7-1] no habrá emparejamiento. Esto lo mostramos a continuación:
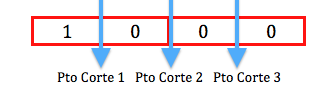
Vemos que en esta generación hay emparejamiento y que además los dos individuos se van a emparejar, así que ahora hay que ver como se emparejan estos dos individuo. Para ello hay que calcular el "punto de corte" del cromosoma sobre el que se va ha hacer el intercambio. Como se muestra a continuación se ve que hay 3 puntos de corte en el cromosoma para que se puedan emparejar:
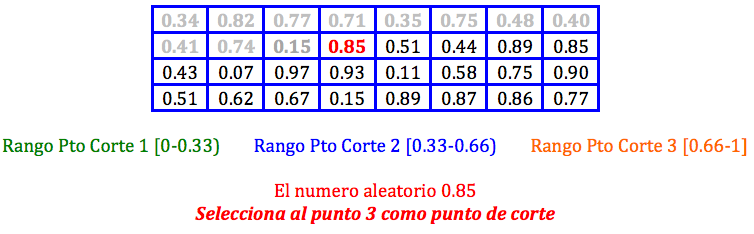
Esto quiere decir que volvemos a crear rangos de selección y seleccionaremos uno de los tres puntos de corte para el emparejamiento. Esta selección del punto de corte lo mostramos a continuación:
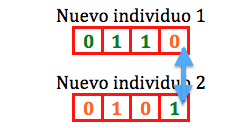
Con todo lo calculado podemos ya generar unos nuevos individuos. Dado que hemos seleccionado como punto de corte al tercer cromosoma, querrá decir que el primer individuo tendrá como valor de la última posición del cromosoma el valor de la ultima posición del cromosoma del individuo 2, lo que quiere decir que el emparejamiento dará como resultado dos nuevos individuos con el intercambio en los valores del cromosoma. Esta intercambio lo mostramos a continuación:
Ya por último queda ver si alguno de los individuos sufrirá alguna mutación. Para ello cogemos un número aleatorio por cromosoma (8 números aleatorio, 4 por cada individuo) y vemos si esta dentro de la probabilidad de mutación, es decir, que si el numero aleatorio esta dentro del rango [0-0.3) el elemento del cromosoma mutará a su complementario y sino esta en ese rango no habrá mutación. A continuación vemos las mutaciones que se producen:
Llegados a este punto ya tenemos una nueva generación de individuos creada que es una generación en la cual tenemos un individuo (individuo 2 con x=1) que es un individuo "mejor" que los de la generación anterior ya que su valor aplicando la función de fitness es de 1,41 tal y como se muestra a continuación:
Tambien vemos que el individuo 1 es peor individuo que sus progenitores. Como podréis observar solamente con una única generación no nos hemos acercado al mejor individuo que seria el individuo con valor x=11 con lo cual necesitaríamos más individuos y hacer esto con muchas más generaciones, es decir repetir este proceso 'n' veces y en la generación 'n' coger el mejor individuo.
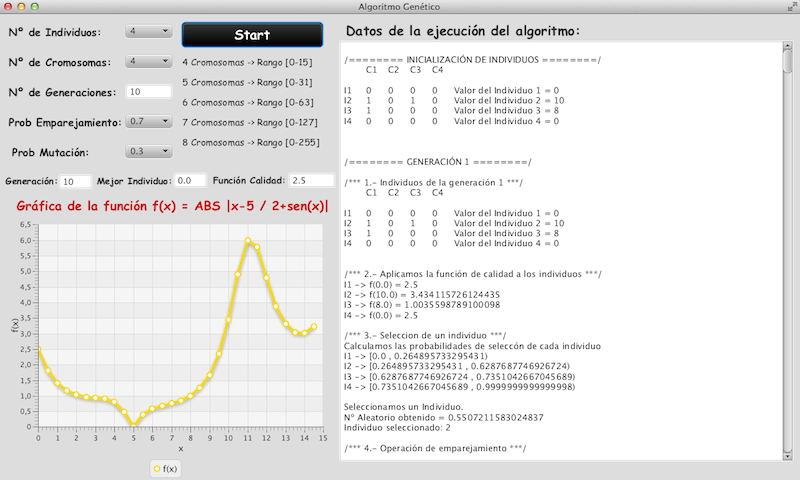
Para que podais "jugar" y ver lo bueno o lo malo que son los algoritmos genéticos se os ha compartido un programa hecho en JAVA (un ".jar" que lo podeis descargar en el enlace del principio de la entrada) en el que se puede resolver este problema poniendo los individuos que se quieran, las generaciones que se quieran, en mas rangos de la función, es decir con individuos representados con más cromosomas y cambiando las probabilidades de emparejamiento y mutación. Tambien se pueden ver todos los detalles y pasos que da el algoritmo genético en cada generación realizada. A continuación os muestro una imagen del programa tras una ejecución:
Cuando hagais alguna ejecución de este programa (tener paciencia para ejecuciones largas porque no lo hice con threads y tarda un poco en dar los resultados) vereis que en la mayoría de las ocasiones no da el mejor resultado por muchas generaciones que le pongáis y por mucho que varieis las probabilidades de emparejamiento y mutación. Como se comento en la entrada "¿Que es la Computación Evolutiva?" los algoritmos genéticos dan unos resultados "decentes" pero no dan (en la mayoría de los casos) el mejor resultado al problema, aunque pueda dar un resultado bastante bueno o no. En esta entrada se ha explicado paso por paso como funciona un algoritmo genético pero CUIDADO para resolver los problemas que tengáis que resolver plantearos otras opciones antes de utilizar un algoritmo genético porque seguramente no sea el algoritmo genético la mejor opción salvo que no tengáis ni idea de abordar el problema.
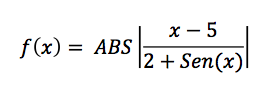


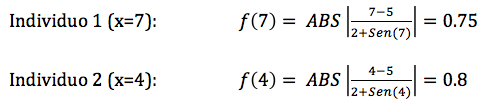


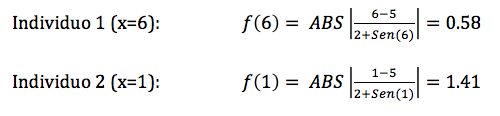
No hay comentarios:
Publicar un comentario