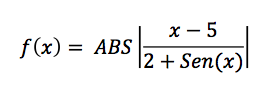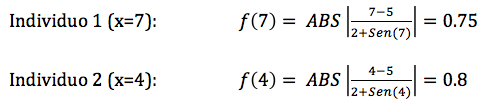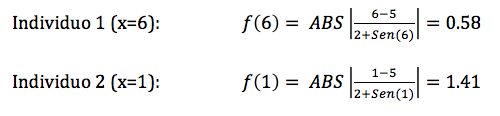Inteligencia artificial: algoritmos genéticos

Mi investigación gira alrededor del modelado, simulación y optimización. Y en principio, en la universidad, la docencia suele ir alineada con la investigación. Así, pertenezco al equipo docente de Computación e Inteligencia Artificial (IA). Pero curiosamente, una de las asignaturas de las que soy responsable* es Biología Molecular (BM). Realmente es una coincidencia interesante porque si bien es cierto que como informático nunca tendré los conocimientos en Biología Molecular que tiene un biólogo, difícilmente no habré oído hablar de Algoritmos Genéticos (AG). Pero ¿qué son y de dónde vienen?

Uno de los campos más interesantes y estudiados de la BM es la genética. A todos nos suenan científicos como Darwin, Mendel, McClintock y conceptos como genoma, mutación, adaptación, etc. Todos ellos, de manera más o menos directa están relacionados con la genética. Pero ¿por qué nos puede interesar a l@s informátic@s? Pues, por la misma razón que observamos a las hormigas, el cerebro humano, o las abejas: todos ellos son sistemas/procesos/… capaces de solucionar problemas complejos. En el caso concreto de la genética nos fijamos en qué mecanismos utiliza la naturaleza para seleccionar individuos y asegurar la persistencia (o no de las especies que conforman). Dándole la vuelta y simplificando, l@s informátic@s recogemos de ésta una serie de mecanismos que evolucionan un conjunto de soluciones, mejorando iteración tras iteración, hasta encontrar las mejores posibles.

Tortuga de las Galápagos 

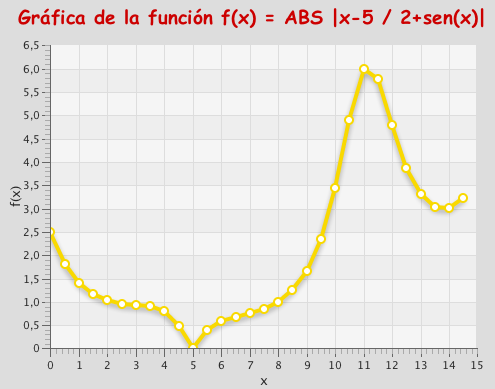
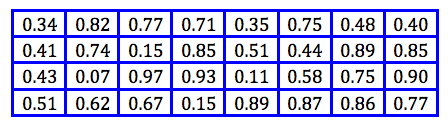
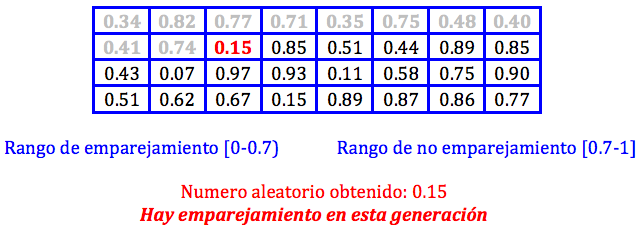
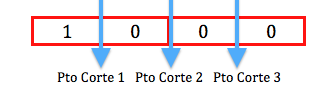
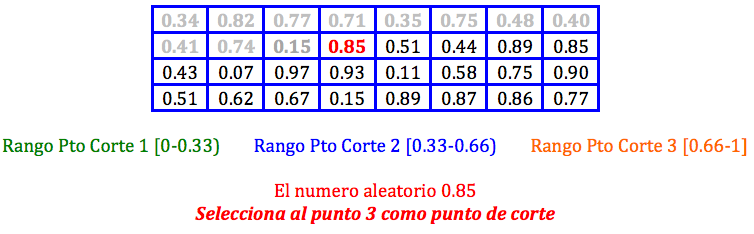
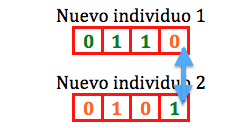
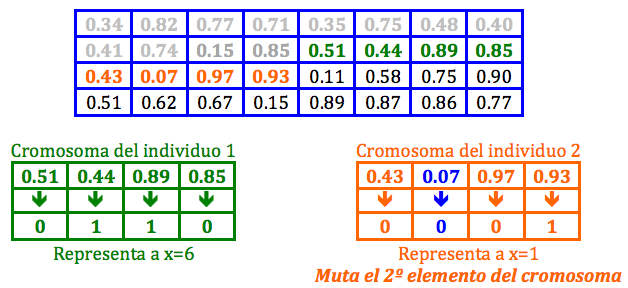
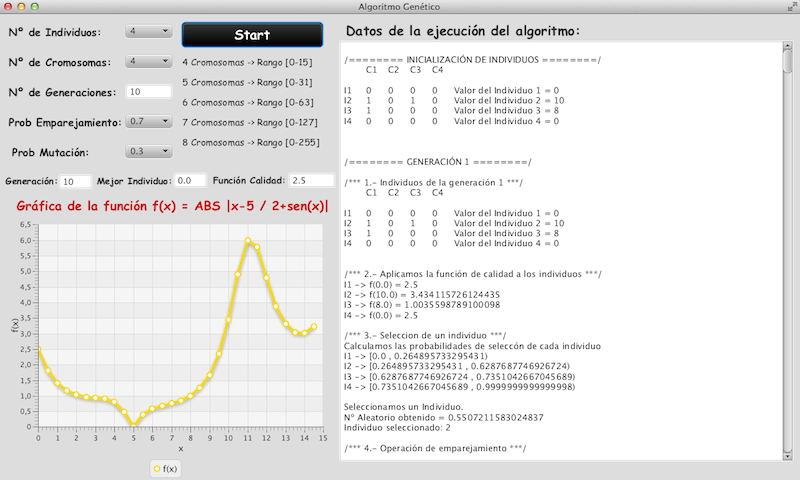
La implementación de la idea de John H. Holland (en los años 70) no es excesivamente compleja: Partimos de una población de individuos, en que cada uno representa una solución factible del problema que se quiere resolver. Cada solución tiene una calidad asociada (fitness) y evidentemente, debe ser factible. En este punto, aplicamos un conjunto de mecanismos evolutivos que producen una nueva generación de individuos. Si todo va bien, tras un cierto número de generaciones, iremos obteniendo individuos (soluciones) que mejoran la solución inicial. Pero ¿cuáles son esos mecanismos? Pues básicamente tres: cruce (simulamos reproducción sexual, por lo que escogeremos parejas de soluciones, las partimos y cruzamos para generar su descendencia), mutación (incluimos mutaciones al azar en los individuos para evitar la convergencia de la población hacia un máximo/mínimo local) y “selección” (eliminamos individuos que representen soluciones no factibles -inviables- y además, en cada generación, nos quedamos con un subconjunto de padres e hijos, normalmente siguiendo el criterio de mejor fitness).  Si como en la realidad este proceso se itera millones de veces (por suerte, los ordenadores nos permiten que los algoritmos genéticos simulen a una velocidad más cercana a la evolución de las bacterias que a la de los primates) nos iremos acercando a una población de soluciones de calidad normalmente muy aceptable.

No debemos olvidar que los Algoritmos Genéticos son metaheurísticas y por lo tanto no hacen una búsqueda completa (exhaustiva) sobre el espacio de soluciones, por lo que no aseguran encontrar la solución óptima. Pero dado que el tipo de problemas a los que se aplican suelen ser de complejidad NP, ya es lo esperado. Estos algoritmos suelen tener pocos parámetros (tamaño de las poblaciones, número de generaciones máximo, probabilidad de mutación, …) pero son extremadamente dependientes del modelado de los individuos (soluciones), ya que es clave facilitar que la producción automática (mediante cruce) de nuevos individuos genere mayoritariamente individuos viables.  También tiene bastante impacto la elección de la población inicial (debido a lo que en BM se llamaría deriva genética, principalmente).

Desde los años 70, los Algoritmos Genéticos han sido una de las “ideas” de la IA más investigadas y utilizadas, dando solución a multitud de problemas combinatorios y siendo utilizadas en aplicaciones reales desde el diseño de los horarios de los JJOO hasta la planificación de rutas logísticas. Y por supuesto, no se han escapado de “sufrir” en sus propios huesos la misma evolución que implementan dando lugar a cientos de aproximaciones y mejoras.

* NOTA: Por suerte, en la UOC, el equipo de las asignaturas no es unipersonal, ya que tenemos colaboradores docentes, que son expert@s en cada asignatura concreta, ya sea por su perfil académico, investigador, o bien su experiencia profesional. En el caso de Biología Molecular, la experta es la Dra. Dorcas Orengo, doctora en Biología y experta en Genética de Poblaciones, Regulación Génica y Genética Molecular Evolutiva.

Daniel Riera es Doctor Ingeniero en Informática por la UAB. Actualmente es el director del Grado de Ingeniería Informática de la UOC y hace investigación dentro del grupo ICSO en temas relacionados con el modelado, simulación y optimización de sistemas combinatorios.

Algoritmos Genéticos – Ejemplo

Para descargar el programa con el algoritmo genético que se muestra en esta entrada, lo podeis descargar pinchando AQUI.

Como ya se vio en el post "¿Que es la Computación Evolutiva?", los algoritmos genéticos son un tipo de algoritmos evolutivos que sirven para resolver problemas de optimización y que se diferencia principalmente de los demás tipos de algoritmos evolutivos por la forma de representar a los individuos, que lo hace por medio de cadenas binarias (Arrays binarios).

En esta entrada vamos a poner un ejemplo de como obtener el máximo de la función que se muestra a continuación en el rango de [0-15] utilizando un algoritmo genético (el argumento del seno de la función se da en radianes). En este ejemplo que ponemos, esta función sera la "Función de Fitness" o función de calidad que utilizaremos en este problema, ya que la 'x' que maximize esta función, sera la mejor solución al problema.

Antes de ver como solucionar el problema, vamos a mostrar en la siguiente imagen la gráfica de esta función para comprobar que el máximo de esta función para el intervalo [0-15] es "x=11" y de esta forma podremos ver lo "bueno o malo" que son los algoritmos genéticos:

El primer "problema" que se nos plantea es "como representar a los individuos" que tendremos en este algoritmo genético. Pues en este caso es muy sencillo y el problema esta planteado adrede para ello. Como en los algoritmos genéticos los individuos se representan con cadenas binarias es muy intuitivo que si queremos encontrar el máximo entre el intervalo [0-15] representemos a los individuos como "números binarios" en este caso como números binarios de longitud 4. Con un numero binario de 4 bits podremos representar 16 números (2^4=16) con lo cual decimos que "los individuos van a estar representados por un cromosoma de longitud 4". Ejemplo:

Una vez llegado a este punto en el que tenemos definida la función de fitness y como representar a los individuos, tenemos que ver: como generamos la primera generación de individuos, como los emparejamos y como mutan. Para realizar todas estas cosas se generará un conjunto de números aleatorios con los que trabajaremos y que veremos su significado a continuación. Para ello y antes de nada deberemos definir con que numero de individuos queremos trabajar, la probabilidad de generación del cromosoma, la probabilidad de emparejamiento y la probabilidad de mutación. Para ver de forma detallada todo este proceso y siguiendo el pseudocódigo mostrado en la entrada de "¿Que es la Computación Evolutiva?" vamos a definir todas estas cosas y ver de forma detallada el transcurso del algoritmo:

1. 1. Longitud del cromosoma: 4
   2. Conjunto de elementos del cromosoma: {0,1}
   3. Número de individuos de la población: 2
   4. Para la creación de la primera generación:
      3.1.- Probabilidad del elemento '0': num aleatorio < 0.5
      3.2.- Probabilidad del elemento '1':  num aleatorio >0.5
   5. Probabilidad de emparejamiento: 0.7
   6. Probabilidad de mutación: 0.3

El conjunto de números aleatorios con los que vamos a trabajar va a ser el siguiente:

En primer lugar vamos a obtener los dos primeros individuos que van a formar la generación inicial. Para obtener los cromosomas de los dos individuos vamos a utilizar los 8 primeros números aleatorios (4 por individuo). Si el numero aleatorio es menor que 0.5 pondremos el elemento '0' al cromosoma y si es mayor que 0.5 le daremos valor '1'. A continuación mostramos como generamos los individuos:

Una vez que conocemos los individuos, aplicamos la función de fitness para que nos diga que individuo es el mejor de los dos y cuanto mejor es uno que otro para ver posteriormente que probabilidad de emparejamiento tiene cada uno:

Como vemos ambos individuos son muy parecidos porque tienen una calidad similar aunque el individuo 2 es un poco mejor que el individuo 1 ya que lo que pretendemos es encontrar el máximo de la función. Ahora pasamos a calcular las probabilidades de cada individuo para el emparejamiento y esto lo hacemos con una regla de tres simple:

Lo que pretendemos con esto es ver que individuos seleccionamos para emparejarse. Para ello cogeremos los dos siguientes números aleatorios y si están dentro de los rangos de selección, ese individuo sera apto para el emparejamiento (en el caso de que haya emparejamiento es esa generación). Esto quiere decir que si sacamos un número aleatorio dentro del intervalo [0-0.48) el individuo 1 se emparejará y si otro numero aleatorio esta en el intervalo [0.48-1] tambien sera apto el individuo 2 para emparejarse. A continuación vemos si son aptos para emparejarse o no:

Con esto vemos que los dos individuos son aptos para el emparejamiento, pero ¿habrá emparejamiento en esta generación?. Para ver si en esta generación hay emparejamiento hay que ver si el siguiente numero aleatorio esta dentro de la probabilidad de emparejamiento que la definimos como 0.7, lo que quiere decir que si el número aleatorio esta en el rango [0-0.7) habrá emparejamiento y si esta entre [0.7-1] no habrá emparejamiento. Esto lo mostramos a continuación:

Vemos que en esta generación hay emparejamiento y que además los dos individuos se van a emparejar, así que ahora hay que ver como se emparejan estos dos individuo. Para ello hay que calcular el "punto de corte" del cromosoma sobre el que se va ha hacer el intercambio. Como se muestra a continuación se ve que hay 3 puntos de corte en el cromosoma para que se puedan emparejar:

Esto quiere decir que volvemos a crear rangos de selección y seleccionaremos uno de los tres puntos de corte para el emparejamiento. Esta selección del punto de corte lo mostramos a continuación:

Con todo lo calculado podemos ya generar unos nuevos individuos. Dado que hemos seleccionado como punto de corte al tercer cromosoma, querrá decir que el primer individuo tendrá como valor de la última posición del cromosoma el valor de la ultima posición del cromosoma del individuo 2, lo que quiere decir que el emparejamiento dará como resultado dos nuevos individuos con el intercambio en los valores del cromosoma. Esta intercambio lo mostramos a continuación:

Ya por último queda ver si alguno de los individuos sufrirá alguna mutación. Para ello cogemos un número aleatorio por cromosoma (8 números aleatorio, 4 por cada individuo) y vemos si esta dentro de la probabilidad de mutación, es decir, que si el numero aleatorio esta dentro del rango [0-0.3) el elemento del cromosoma mutará a su complementario y sino esta en ese rango no habrá mutación. A continuación vemos las mutaciones que se producen:

Llegados a este punto ya tenemos una nueva generación de individuos creada que es una generación en la cual tenemos un individuo (individuo 2 con x=1) que es un individuo "mejor" que los de la generación anterior ya que su valor aplicando la función de fitness es de 1,41 tal y como se muestra a continuación:

Tambien vemos que el individuo 1 es peor individuo que sus progenitores. Como podréis observar solamente con una única generación no nos hemos acercado al mejor individuo que seria el individuo con valor x=11 con lo cual necesitaríamos más individuos y hacer esto con muchas más generaciones, es decir repetir este proceso 'n' veces y en la generación 'n' coger el mejor individuo.

Para que podais "jugar" y ver lo bueno o lo malo que son los algoritmos genéticos se os ha compartido un programa hecho en JAVA (un ".jar" que lo podeis descargar en el enlace del principio de la entrada) en el que se puede resolver este problema poniendo los individuos que se quieran, las generaciones que se quieran, en mas rangos de la función, es decir con individuos representados con más cromosomas y cambiando las probabilidades de emparejamiento y mutación. Tambien se pueden ver todos los detalles y pasos que da el algoritmo genético en cada generación realizada. A continuación os muestro una imagen del programa tras una ejecución:

Cuando hagais alguna ejecución de este programa (tener paciencia para ejecuciones largas porque no lo hice con threads y tarda un poco en dar los resultados) vereis que en la mayoría de las ocasiones no da el mejor resultado por muchas generaciones que le pongáis y por mucho que varieis las probabilidades de emparejamiento y mutación. Como se comento en la entrada "¿Que es la Computación Evolutiva?" los algoritmos genéticos dan unos resultados "decentes" pero no dan (en la mayoría de los casos) el mejor resultado al problema, aunque pueda dar un resultado bastante bueno o no. En esta entrada se ha explicado paso por paso como funciona un algoritmo genético pero CUIDADO para resolver los problemas que tengáis que resolver plantearos otras opciones antes de utilizar un algoritmo genético porque seguramente no sea el algoritmo genético la mejor opción salvo que no tengáis ni idea de abordar el problema.

3 INCREIBLES ALGORITMOS GENÉTICOS EN C# - UNITY

¿Qué es un algoritmo genético?

ALGORITMOS GENÉTICOS ´ 

1 Introducci´on 

Los Algoritmos Gen´eticos (AGs) son metodos adaptados que pueden usarse para resolver problemas de busqueda ´ y optimizacion. Est´an basados en el proceso gen´etico de los organismos vivos. A lo largo de las generaciones, las poblaciones evolucionan en la naturaleza de acorde con los principios de la seleccion natural y la supervivencia de los m´as fuertes, postulados por Darwin (1859). Por imitaci´on de este proceso, los Algoritmos Geneticos son capaces de ir creando soluciones para problemas del mundo real. La evolucion de dichas soluciones hacia valores optimos ´ del problema depende en buena medida de una adecuada codificacion de las mismas. Los principios b´asicos de los Algoritmos Gen´eticos fueron establecidos por Holland (1975), y se encuentran bien descritos en varios textos – Goldberg (1989), Davis (1991), Michalewicz (1992), Reeves (1993) – . En la naturaleza los individuos de una poblacion compiten entre s´ı en la busqueda ´ de recursos tales como comida, agua y refugio. Incluso los miembros de una misma especie compiten a menudo en la busqueda ´ de un companero. ˜ Aquellos individuos que tienen m´as ´exito en sobrevivir y en atraer companeros ˜ tienen mayor probabilidad de generar un gran numero ´ de descendientes. Por el contrario individuos poco dotados produciran un menor numero ´ de descendientes. Esto significa que los genes de los individuos mejor adaptados se propagar´an en sucesivas generaciones hacia un numero ´ de individuos creciente. La combinacion de buenas caracterısticas provenientes de diferentes ancestros, puede a veces producir descendientes “superindividuos”, cuya adaptaci´on es mucho mayor que la de cualquiera de sus ancestros. De esta manera, las especies evolucionan logrando unas caracter´ısticas cada vez mejor adaptadas al entorno en el que viven. Los Algoritmos Geneticos usan una analogıa directa con el comportamiento natural. Trabajan con una poblaci´on de individuos, cada uno de los cuales representa una soluci´on factible a un problema dado. A cada individuo se le asigna un valor o´ puntuacion, relacionado con la bondad de dicha solucion. En la naturaleza esto equivaldrıa al grado de efectividad de un organismo para competir por unos determinados recursos. Cuanto mayor sea la adaptacion de un individuo al problema, mayor ser´a la probabilidad de que el mismo sea seleccionado para reproducirse, cruzando su material gen´etico con otro individuo seleccionado de igual forma. Este cruce producir´a nuevos individuos – descendientes de los anteriores – los cuales comparten algunas de las caracterısticas de sus padres. Cuanto menor sea la adaptacion de un individuo, menor ser´a la probabilidad de que dicho individuo sea seleccionado para la reproduccion, y por tanto de que su material gen´etico se propague en sucesivas generaciones. De esta manera se produce una nueva poblaci´on de posibles soluciones, la cual reemplaza a la anterior y verifica la interesante propiedad de que contiene una mayor proporcion de buenas caracter´ısticas en comparaci´on con la poblaci´on anterior. As´ı a lo largo de las generaciones las buenas caracter´ısticas se propagan a trav´es de la poblaci´on. Favoreciendo el cruce de los individuos mejor adaptados, van siendo exploradas las areas ´ m´as prometedoras del espacio de busqueda. ´ Si el Algoritmo Genetico ha sido bien disenado, ˜ la poblaci´on converger´a hacia una soluci´on optima ´ del problema. El poder de los Algoritmos Gen´eticos proviene del hecho de que se trata de una t´ecnica robusta, y pueden tratar con ´exito una gran variedad de problemas provenientes de diferentes areas, ´ incluyendo aquellos en los que otros m´etodos encuentran dificultades. Si bien no se garantiza que el Algoritmo Gen´etico encuentre la soluci´on optima ´ del problema, existe evidencia emp´ırica de que se encuentran soluciones de un nivel aceptable, en un tiempo competitivo con el resto de algoritmos de optimizaci´on combinatoria. En el caso de que existan t´ecnicas especializadas para resolver un determinado problema, lo m´as probable es que superen al Algoritmo Gen´etico, tanto en rapidez como en eficacia. El gran campo de aplicaci´on de los Algoritmos Gen´eticos se relaciona con aquellos problemas para los cuales no existen t´ecnicas especializadas. Incluso en el caso en que dichas t´ecnicas existan, y funcionen bien, pueden efectuarse mejoras de las mismas hibrid´andolas con los Algoritmos Gen´eticos. La estructura de este cap´ıtulo es como sigue: en la siguiente secci´on se introduce por medio de 1 un ejemplo el denominado Algoritmo Gen´etico Simple, tambi´en conocido como Algoritmo Gen´etico Can´onico, para a continuaci´on, mostrar distintas extensiones y modificaciones del mismo, relativas a los operadores de selecci´on, cruce, mutaci´on y reducci´on, as´ı como a la hibridaci´on del Algoritmo Gen´etico con otros algoritmos de busqueda ´ local, y a diversos modelos de Algoritmos Gen´eticos Distribuidos. En la siguiente secci´on nos preguntamos el motivo por el cual funcionan los Algoritmos Gen´eticos, demostr´andose el teorema de los esquemas, y referenci´andose algunos trabajos te´oricos relacionados con las condiciones suficientes para garantizar la convergencia de dichos algoritmos hacia el optimo ´ global. Finalizamos el cap´ıtulo, mostrando operadores de cruce y mutaci´on espec´ıficos